Music of moons
The fact that neither Newton's nor Einstein's theory of gravitation accounts for the many astronomically observed (and statistically significant) synchronicities and resonances that exist between the orbital and rotational periods of planets and moons points to a gap in our understanding of celestial motion.
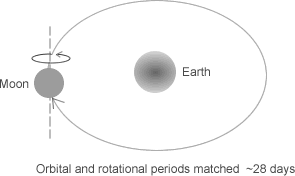
The Apollo space missions allowed humankind for the first time to see 'the other side of the moon' (since the moon always presents the same face to us here on planet Earth). But it appears we have seldom pondered why this is so. It is easy, upon a brief consideration of the situation as we understand it today, to realise that the moon must take exactly the same time to spin once on its own axis as it does to orbit once around the Earth—28 days. But this does not explain why the moon has apparently tuned in to a 1:1 resonance between its orbital and rotational periods.
The [more general] pattern appears to be that planets and moons tend to lock in to periods which are whole number ratios of one another*, closely analogous to a musical scale, or to the harmonious intervals on a vibrating string. For instance, three of Jupiter's largest moons , Io, Europa, and Ganymede, orbit the planet as follows: for every one orbit by Ganymede, Europa orbits Jupiter twice, and Io orbits Jupiter four times. This is actually known as a 4:2:1 resonance . |
|
Such patterns and whole-number ratios manifesting in the relative rotational motion of moons and planets are further examples from Nature of what I am calling 'resonant scale structures'.
| back to top |
next > |