Introduction to the equitriangular unit of area (the etu)
This web page is quoted from the author's book Principles of nature; towards a new visual language, WA Roberts P/L Canberra. 2003.pp. 108-109 [Used with permission of the author] ~ slightly edited/reformatted for the web.
Let an etu be a specific but relative unit of area:
Its absolute value may change, but it is defined to be always the area of an equilateral triangle of unitary side length.
Thus if the area of an equilateral triangle is defined to be 12 etu, or more simply as 1 etu (i.e. 1 x 1, a unit of area), then its side-length is, by the same definition, 1 unit (i.e. one unit of length). The reverse is also true: If an equilateral triangle has sides of length 1 unit, its area is by definition, 1 etu.*
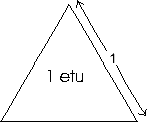
...for the time being, we shall refer to the new unit as an ‘etu’ in order to differentiate it from p2 numbers in square form (or for that matter, those of hexagonal form, etc).
The important point here is that units are related to other units, and, more particularly, that 'harmonics' exist as much in the field of mathematics and geometry as in music. Certain units 'mark out' resonances in the 'population of numbers and geometries'. (The beautiful connections and resonances will become apparent as we enter through this gateway).
| back to top |
next > |