Principles of Nature: towards a new visual language
Resonances among the parametric equations for generating Pythagorean, Eutrigon, and Co-eutrigon Triples
This web page is reproduced from the author's book Principles of nature; towards a new visual language, WA Roberts P/L Canberra. 2003.p.148 [Used with permission], Edited, reformatted and annotated for the web by the author.
We have found that the equilateral triangle exhibits ‘square symmetry’ in that it can always be divided into a p2 number of smaller self-similar parts.
But in the classical tonal system of music, the unit of the octave was cleverly divided into twelve equal smaller intervals (or parts) by JS Bach , and that’s why his tuning of the keyboard this way was called ‘even-tempered’ (in other words, divided ‘equally’). Twelve is certainly not a square number! Or is it? It is certainly more than of passing note, that the equilateral triangle ... is one of the most resonant shapes for numbers of the form p2 (and traditionally known simply as ‘the squares’). More surprising still is that it is just as easily divided into twelve equal parts (or ‘semitones’). An example of such a division is shown in figure 97.
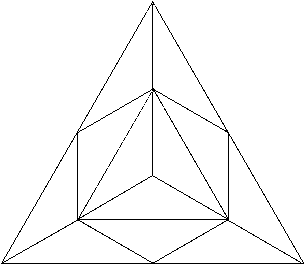
Figure 97
Here an equilateral triangle, which may stand for a musical equivalent of the octave , is divided into twelve equal parts (the musical equivalent of the semitone ). There are many harmonics within this figure: there is an internal equilateral triangle, an internal hexagon, and resonances of ‘the semitone’ (similar isosceles triangles).
Intriguingly, seen in a related musical way, the outer equilateral triangle contains a smaller equilateral triangle whose area is one quarter the area of the outer all-encompassing equilateral triangle and whose side-length is one half of the side-length of the outer equilateral triangle (which is again strongly reminiscent of the octave in music and how it coincides with a halving of a vibrating string’s length...
The centrally inscribed hexagon of figure 97 is composed of six of the twelve congruent isosceles triangles, and it therefore occupies one half of the figure’s total area—in this way, it is like an ‘octave of areas’. It follows that the remaining six isosceles triangles (unshaded and with dashed outline in fig. 98) occupy the same area as that of the shaded central hexagon and therefore may be rearranged in the same way to form a separate hexagon of identical area to the first (fig. 98-right).
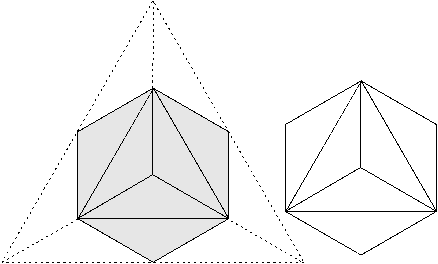
Figure 98
These two hexagons (derived from the original figure) may alternatively be more classically divided into six equilateral triangles. Again there are ‘twelve semitones ’, each of exactly the same area as one isosceles triangle of the original figure but of a different symmetric shape and spread over two identical hexagons. (cf. figs. 98 & 99).
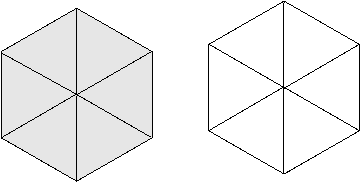
Figure 99
This transformation is also strongly reminiscent of the ‘modulation between keys’ within music based on the diatonic scale. Moreover it resonates with the process of mitosis in biochemistry—the way a cell divides and replicates to form two new cells with the same complement of chromosomes. Although the shape has changed (from an equilateral triangle to a hexagon) the new scale-structure paradigm accepts this as a natural ratio or resonance of the system...p2 numbers can be geometrically represented in one of three regular polygonal forms within Euclidean geometry: as equilateral triangles, squares, or hexagon s.... Traditionally, these numbers have been seen almost exclusively as squares. So the transformation from an equilateral triangular ‘cell’ into two regular hexagonal ‘cells’ makes sense from the scale-structure perspective, and these shapes are seen as simply alternative forms of the same number.
Now we will divide these first generation hexagonal ‘cells’ (or ‘complete another octave’ to use the musical metaphor) and, in so doing, form four second generation ‘cells’ (fig. 100-middle row). We will do this by once more modulating the internal division of the hexagons back into six congruent isosceles ‘semitone -triangles’ (fig. 100-upper), then by regrouping these apex-to-apex to form four sets of three isosceles triangle (fig. 100-second row), each of which recapitulates the equilateral triangular form of the original (fig. 97).
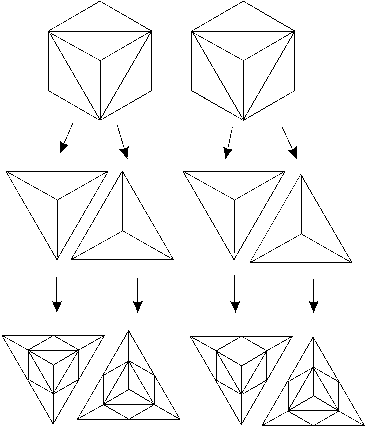
Figure 100
...
Escher has completed a huge body of work in exploring transitional systems that interlink different forms of symmetry and regular division in the Euclidean plane (and we do not repeat it here), but the interested reader is referred to Schattschneider ’s outstanding survey of Escher’s work in symmetry and the division of the plane. (D. Schattschneider, 1990)
Greg Frederickson is an expert in this huge and fascinating field of geometric dissections and tessellations of the plane. He has amassed a huge number of fascinating geometric dissections, many his own, and many others from around the globe.(GN Frederickson, 1997). Readers interested in this area are encouraged to buy or look up his books as well as Schattschneider's scholarly survey of Escher's work (D. Schattschneider, 1990) on the regular division of the plane.
Same figures, but here reflecting the ‘cell division’ metaphor
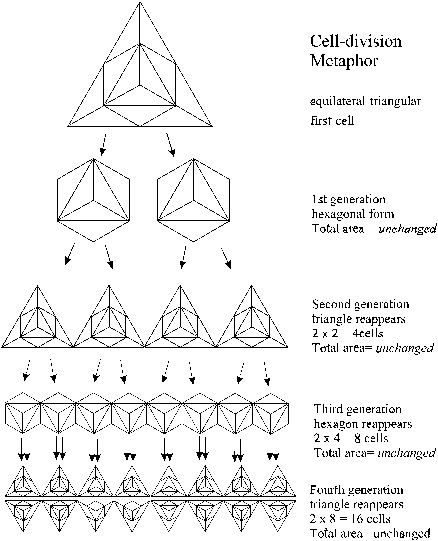
Figure 102
In the successive generations of ‘cells’ in figure 102, there is an alternation between triangular and hexagonal forms. This seems far removed from the biochemistry of cellular division, yet scale structure theory sees the equilateral triangle as a member of a highly-interconnected and resonant scale structure—one of only three regular polygons which can tile the Euclidean plane—and moreover that there exist compelling links between geometry and number, and between these and the dynamics of Natural phenomena. It is not unreasonable to conjecture that this ‘geometric progression’ may find a resonance in the actual dynamics of cellular division, and may be efficacious within the context of medical research, in particular the study of cellular division and replication. Such a conjecture is based on scale-structure theory and the Principle of Universal Interconnectedness.
Fig.103 |
In our number–system, in which each number follows from the former by the addition of one unit there is a resonance of this oscillation between triangular and hexagonal forms, as depicted in fig. 102, in that the successive integers oscillate in this way: odd, even, odd, even, (fig. 103). Each step involves the same process (the addition of one unit) but results in an integer of one then the other type (odd then even) which echo the alternation between triangles and hexagons (fig. 102). In the biochemistry of cellular division, it is conceivable (if not already discovered) that mitoses (somatic cellular divisions) reflect, in some way, this oscillatory phenomenon in that successive divisions may not result in exactly the same form of the genetic material (even though the full complement of chromosomes is replicated at each division); whereas jumping two generations at a time may reproduce not only the same complement of the chromosomes, but also some other congruity or synchronicity of forms. |
The 1: 3 ratio of squares and octaves
In concluding this section, we will turn to consider the p2 (or ‘square’) nature of the equilateral triangular construction of figure 97. In it, the equilateral triangle is divided into twelve identical isosceles triangles which we likened to the twelve semitones of the western diatonic scale. To the left of figure 104 the original arrangement of the semitone-like isosceles triangles of figure 97 is reproduced. To its right are the same triangles, except that this time the central hexagon has been simply rotated by 60°. In the arrangement on the right we can more easily see the p2 (or so-called square) property of the equilateral triangle, and which is indicated below, in figure 105.
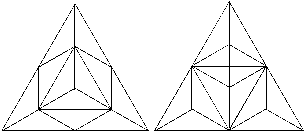
Figure 104
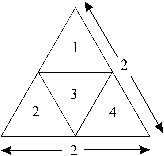
Figure 105
p2 numbers are just as much triangular as they are square.
Here 2 x 2 = 4.
We continue with a musical scale-like exploration of various combinations or intervals of ‘tones’ and ‘semitones’ and, which together, reconstitute our ‘octave’ (the outer equilateral triangle). Join three of the small ‘semitone triangles’ in the lower left corner (shaded in fig. 106-right) to form an internal equilateral triangle which is one quarter of the ‘octave’ or area of the outer equilateral triangle (cf. fig. 105).
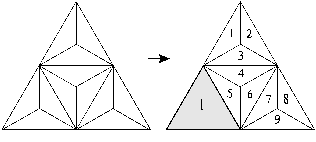
Figure 106
Nine isosceles ‘semitone-triangles’ constitute the remaining area.
Figures 98 & 99 demonstrated another way of dividing paired ‘semitone triangles’ (joined along their longest side) to form two congruent equilateral triangles. That is possible because these isosceles ‘semitone triangles’ are special co-eutrigons... having not only a defining 120° angle but also, since they are isosceles, their other internal angles are each 30°. When two are joined along their longest sides to form a diamond shape, the figure thus formed is a rhombus (a parallelogram with four equal sides). This rhombus is special in that the larger internal angles are 120° and the smaller ones, 60°. It may therefore remain longitudinally divided (composed of two isosceles co-eutrigons, figure 107-left), or transversely divided to form two equilateral triangles (fig. 107-right). I shall name this special resonant class of rhombus, which is formed by the conjoining of two equilateral triangles, a 'diamond'.
Each of its component triangles (the isosceles co-eutrigon and the equilateral triangle) has the same area since the same rhombus is formed by a pair of either.
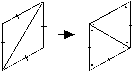
Figure 107
The remaining nine numbered isosceles triangles of figure 106 may thus be alternatively divided as in figure 107-right and the nine congruent equilateral triangles rearranged to form another equilateral triangle
(figs. 108–109, since 3 x 3 =9, which is a p2 number). In Section 2, it was demonstrated that p2 numbers can always be represented in equilateral triangular form (amongst other polygons) and not just as squares.
An alternative resonant internal division of the remaining nine ‘semitone triangles’ of figure 106 is hinted at by the dashed lines of figure 108 which indicates alternative lines of division, and solid dots which indicate turning–points of rotation (showing how halves of an isosceles co-eutrigon triangle can be rotated about the midpoint of its base to form an equilateral triangle of the same area).
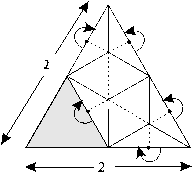
Figure 108
![]()
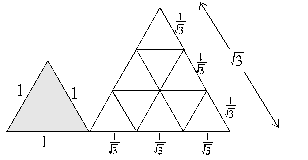
Figure 109
Area of left triangle = 1 etu. Total unshaded area = 3 etu. Total area of combined figures is 4 etu.
...figure 109 begins to highlight some irrationalities of our current number system in that we get √3 turning up as the side-length of the equilateral triangle on the right. See “Conclusion” that follows this section for further discussion.
...
The points to be drawn from figures 106–109 are:
-
An equilateral triangle can generically represent any p2-number (traditionally known as ‘square numbers’).
-
The resonant division and reconfiguration of the equilateral triangle of figure 108 to form two equilateral triangles in the integral ratio 1 : 3 (fig. 109) shows a geometric form of rationalism in which the original regular polygon is divided ‘integrally’ to form two self-similar smaller identical polygons in geometric proportion, but which is not reflected by our number notation since we obtain an irrational number ( √3 ) for the side-length of one of these .
From point 1 above, we may generalise figure 108 to represent any so-called square number (of the form p x p):

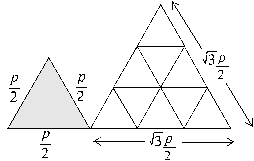
Figure 111 -
Any equilateral triangle of side-length p (and whose area in etu is thus p2), has an area which is the sum of two smaller equilateral triangles in the ratio 1: 3 (or, whose areas are ¼ and ¾ the area of the original) See figure 111. This may be expressed as,
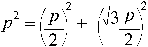
-
Although some may object that the areas are rational but not the side-lengths of the figure (and therefore, ‘So what? Because the numbers add up anyway’), plainly, the geometry speaks for itself, and in a language which our number-system cannot yet adequately translate. Firstly, the areas of each smaller triangle are in the integral ratio, 1 : 3. Secondly, the original figure (figs. 106 ff.) has been ‘rationally divided’. Thirdly, the numerical values for the sides of the right-hand triangle (figs.108–109) that our current number-system returns are irrational numbers, and this seems to grate against the geometry in that the sides of that triangle are divided into exactly three equal units of length. Furthermore, these three units of length in the right-hand equilateral triangle of figure 109 differ from the single unit of side-length of the left-hand triangle yet each arises logically from the scale structure of the original figure 102. This implies a relative unit of length. And this is precisely what is missing from our number-system: its inflexible ‘absolutism of units’ is the root of irrationality.
-
The geometric scale structures of figs. 108–111 link up rather wonderfully with the Pythagorean Theorem, but with a twist. We find a ‘square number’ which is broken down into the sum of two other square numbers (or, more precisely, an equilateral triangle which is the sum of two smaller equilateral triangles in the ratio, 1 : 3). Thus a2 + b2 = c2. But there is the additional criterion of the ratios: that b2 = 3a2. And therefore that c2 = 4a2. A generic fourfoldness of squares is thus revealed. This is no surprise from the scale-structure point of view since all p2 numbers ... may also be expressed in square form. So too, it rings other ancient bells—not least, the tetraktys of the Pythagoreans.
| Visual music will depend upon a synchronisation and resonance of many parts and wholes and upon a radical rethink of how we can more harmoniously relate the units of geometry and number. |
|