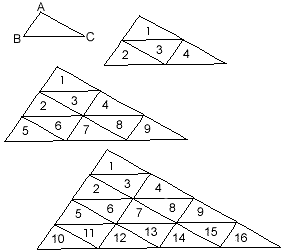
Triangular units of area:
in a more concordant geometry of relativity
Any scalene triangle can be dissected into a so-called 'square number' of similar unit-triangles
|
Figure 65 (figure numbers correspond to the book numbering) demonstrates that successively larger triangles generated by p2 configurations of these smaller scalene units are geometrically similar to the original scalene triangular unit from which they were constructed (i.e. their angles are equal, and their sides are in the same ratios, since all sides of the unit triangle ABC are successively multiplied by 2, 3, 4, etc to yield the triangles above). This means in effect, that the p2 side-symmetry of the square and equilateral triangle is maintained here, but with a twist. For example, in the final 16-part triangular arrangement above (representing the 42-configuration ), the overall triangular shape can be seen to have all sides divided into four units of length (as in a 4 x 4 square), but now (and here's the twist) the unit of length has also become relative rather than absolute. The units-of-length on each side are side-specific (or in other words, side-relative). The asymmetry of the scalene triangle has imposed the need to 'match side with unit-triangle side' in order to maintain this square-like property and composition. In other words four units-of-length on one side of the triangle do not, in an absolute sense, equal four units-of-length on another side of the same triangle, only in a relative sense, relative to the respective sides of the scalene-triangular-unit as given above. The numbers are equal, but the lengths are relative.
Therefore if the scalene triangular units of length are viewed in this relative way, they too exhibit the characteristics and symmetries of the ‘square numbers’, including the ability to tile the plane without gaps.
The area of a scalene triangle in self-similar scalene units is thus also p2, where p is the side-relative length stated in terms (and multiples) of the length as given by the scalene triangle unit’s respective side.
Another interesting connection between 'squares' and triangles
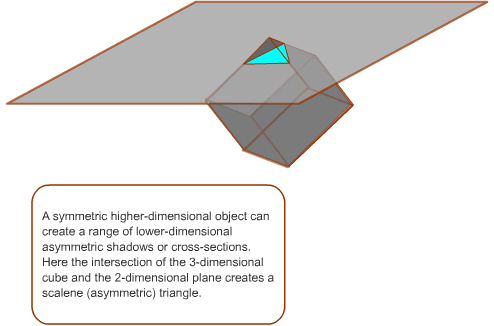
A scalene triangle (coloured blue in the diagram below) in the Euclidean plane can be represented as a cross-section through a cube.
Email contact/feedback W Roberts
| back to top |
next > |