This section is based on sections of my book (W. Roberts, 2003, pp. 84-89), edited and reformatted with supplementary commentary for the web..
Examples of some scale-structures now available for syntactical exploration within ‘covert scale structure compositions’
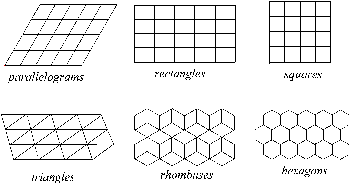
- The six fundamental regular divisions of the plane , including ‘transitional systems’, as explored and developed by Escher (D. Schattschneider, 1990. pp. 31—33) in his brilliant pioneering work and briefly discussed above. The twist now is that these fundamental geometries can be algorithmically or in other ways linked to the overt image. Also his working out of transitional systems can be taken as a platform upon which might be built a new syntax of moving visual forms and modulating geometries.
- Conserved areas of polymorphic and asymmetric forms (and, by implication, conserved volumes of three-dimensional forms) - this is related to the aforementioned scale-structure but an extension of it. (See also the author’s painting Magic Square, 1995, in Gallery of selected works by the author)
- Scale-of-lines/‘gene pool’: This is something that I developed 1995-1996 in an effort to obtain new ways of creating a covert familiality of forms in abstract composition, and new covert scale structures more generally. (These scales of lines used in a composition are analogous to a gene pool and we might therefore call the resultant compositions, ‘genetic compositions’.) A scale of lines (created intuitively or according to higher-level principles) limits the number of basic line elements or ‘phonemes’ available to the artist, which are then employed (expressed) variously, both intuitively and according to yet other scale structures which act as determinants of space or position [See paintings Gene Pool (1996) and, Magic Square (1995-1996), in Gallery of selected works by the author]
- Covert scales of colour: There have been numerous divisions of the colour spectrum into various scales in the history of art —see Colour and Culture (J Gage, 1993). It might now be possible to find renewed application for some of these. In 1995, I developed a colour scale based on a modulation of light intensity (tone or value) into a spectral-equivalent colour at full strength. (See the painting, Low Tide, Cancale, and Astronomer’s Day in the section, Gallery of selected works by the author.) The effect is to use colour itself as a metaphor for light...
- Systems of asymmetric balance: These are less geometric ways of bringing balance into a work as a whole, but asymmetrically. In my painting Magic Square 1995-1996 (refer to image of painting and accompanying text later in this section) there is an underlying system of asymmetric balance employing three underlying covert scale structures which unify the composition. This particular system of asymmetric balance is that the composition is based on the [ancient Chinese] Lho Shu magic square arrangement of the numbers one through nine.
- iterative functions / ‘fractal’ image generation In these, an operation (usually a mathematical function) is re-run billions of times using the generated outputs or answers of each cycle as new inputs. (The Mandelbrot Set is probably the most famous and still one of the most beautiful of these, named after its discoverer, Benoit Mandelbrot, who also coined the term ‘fractal’ to describe this sort of image*.) This generates extremely life-like forms with complexity that can be 'magnified' to reveal ever-unfolding levels of complexity within complexity (just as in nature), and recapitulations of recognizable forms, but with subtle variation. Fractal images are excellent examples of one type of covert scale structure art. These operations can now be combined with other covert scale structures and syntactical operations to spawn even greater diversity and complexity. Also, tertiary scale structures may be able to be linked together to form quaternary scales yielding nested orders of orders—harmonics of basic frequencies and scale structures that unfold to infinity.
- mathematical functions or operations applied to any aspect or field of elements in visual composition. This is potentially limitless and may include other scale structures as subsets
- syntactical rules designed to covertly and asymmetrically connect forms and positions—to direct metamorphoses in dynamic visual symphonies—a grammar of visual forms and events. These rules will 'determine', and be determined. Provisional scale structures are their determinants. Resonant scale structures are their 'attractors'. As these resonant scale structures are increasingly found and adopted as part of the syntax, the language will become much more powerful. This grammar or syntax could be varied globally as in languages today, but more importantly, it may be possible to achieve a language of a more generic grammar and syntax. This language could foreseeably interconnect many languages as we know them today.
- syntaxes that include time [rhythms, choreography]: allowing integration of animated abstract visual art with music. Irregular syntactical aspects will closely relate to what we now understand as 'style': the phraseology, the irregular but conscious and subconscious organisation and expression; the combinations of associative and dissociative aspects of composition. The discovery of various resonant scale structures linked mathematically and syntactically, and subsequently manipulated according to yet other emergent scale structures could lead to new systems of abstract thinking.
Thinking is necessarily an associative activity and the assimilation of resonant scale structures could empower thought and simplify memory because scales can be stored more efficiently by the brain.
We can try new divisions and combinations; we can discover new resonant scale structures linking them syntactically to create new languages. These will enable us to see and think in new ways. The question becomes not: Are there other scale structures to discover? But: How and where may they be found? And, realising that information or content is active upon the mind: How can they 'find' us? The answer, in light of the current discussion, would appear to be that when we are conscious of 'them', they become'conscious' of us. In the words of Krishnamurti , ‘Consciousness is its content.’(as cited in D. Reanney, 1994, p. 65). When we become conscious of a greater whole of which we are part, we become part of a greater consciousness in which we are whole. |
|
Magic squares are mathematical square arrangements of sequences of numbers such that all columns, rows and the two main diagonals sum to the same number (in this instance, 15). Yet each number in the sequence (e.g. the numbers 1 to 9 as used in the Lho Shu ) is uniquely represented. The ancient Chinese revered the Lho Shu as perfectly balanced. This balance collapses upon any division: it is a holistic balance. These magic squares and other systems of asymmetric balance can be algorithmically linked to the surface forms and composition in such ways as, for example, ‘numbers of shapes’ or ‘distribution of tones’ etc.