Eutrigon and Co-eutrigon Triads
This web page is reproduced from the author's book Principles of nature; towards a new visual language, WA Roberts P/L Canberra. 2003. pp.137—148, [Used with permission of the author] edited and reformatted for the web, with some additional commentary for the sake of contextual clarity.
Just as the Pythagoreans found a method of generating triads or triples of whole numbers that could form right triangles, scale structure theory implies there ought also to exist similar methods for generating eutrigon and co-eutrigon triads in integral (whole number) sides—that is, whole number solutions for a, b, and c in the equations ab = a2 + b2 – c2 and ab = c2 – a2 – b2 respectively.
Such parametric equations do exist for the eutrigon and co-eutrigon, but before we look at them, we will approach the question by first considering specific examples—those of eutrigons and co-eutrigons in the smallest possible integral sides (much like the corresponding 3–4–5 right triangle in the family of Pythagorean Triples). By combining these to form symmetric wholes (a scale structure approach) we will consider the dynamics and relationships of the component parts, and elucidate the nature of those dynamics and relations in more general (algebraic) terms.
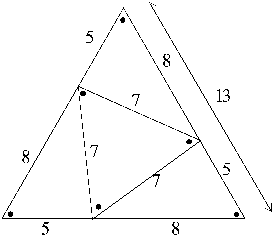
The simplest Eutrigon Triples (those of the lowest integral values for their side lengths) are shown in [the figure below]. It will be noted that such Eutrigon triples must always be paired, because for every eutrigon there exists a ‘complementary eutrigon’ which may, when placed hypotenuse to hypotenuse with the former, complete an equilateral triangle. The two Eutrigon Triples of lowest integral sides [and which form a pair such as described above] are 3-8-7, and 5-8-7. [By convention, we shall state the hypotenuse last in such triples.]
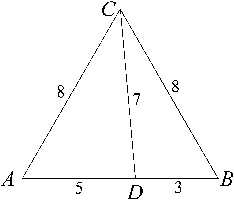
It can be seen from an inspection of [the figure above] that it consists of two conjoined eutrigons whose defining 60° angle is at CAD and CBD respectively, and which have a common hypotenuse, CD, whose value in this instance is 7. Together they form the equilateral triangle 
ABC. These paired eutrigons differ only in the length of one their sides, and in such a way that the ‘variant legs’ sum to give the length of the other side (and equal in both). Thus in [the figure above], we note that 3 + 5 = 8.
A quick check of the eutrigon [to] the left ...shows that the numbers and corresponding areas in etu are indeed in the relation as stipulated by the Eutrigon theorem and as illustrated [below].
By the Eutrigon Theorem, ab = a2 + b2 – c2, (where c is the hypotenuse), thus in the example shown below [a= 5, b=8, c=7] we have, (5 x 8) = 52 + 82 – 72. [Substitution confirms that, 40 = 25 + 64 – 49]
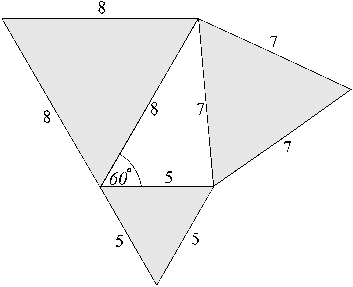
Referring back to eutrigon CBD [in the uppermost figure], which when added to the [other eutrigon] completes an equilateral triangle, we find the Eutrigon Theorem again holds true for the alternative value in which a = 3 (and where the other parameters remain unchanged: b= 8, c = 7). Substitution of these parameters into the Eutrigon Theorem, ab = a2 + b2 – c2, this time gives,
(3 x 8) = 32 + 82 – 72
24= 9 + 64 – 49
24= 73 – 49
Note that in Eutrigon Triples, the hypotenuse of the paired eutrigons (common to both) is also a cevian* of the equilateral triangle formed by the pairing of the eutrigons in this way. Also, note that this cevian [ CD in the figure above] divides one side-length of the equilateral triangle into integral segments (in this case it divides the side-length of 8 units into two segments: one of 5 units and the other of 3 units, 3 + 5 =8).
This division of an equilateral triangle into two eutrigons of integral areas [as measured in terms of relative units of area] and integral side-lengths has implications for the whole notion of ‘rational numbers’, and calls into question the age-old concept of what constitutes a ‘rational number’ or (ipso facto) an ‘irrational number’—old concepts challenged by a new geometric understanding of: numbers, relative units, and spatial division.
Generalising the paired eutrigon construction
We may generalise the paired eutrigon construction [above] and which together form an equilateral triangle....
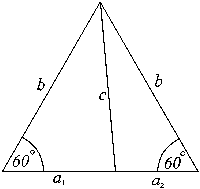
Figure EP1
Note that since the main outer triangle
is equilateral, a1 + a2 = b
By the Eutrigon theorem (algebraic form) we have equations for the two internal eutrigons as follows,
a1b = a12 + b2 – c2 . . . . . . . . . eutrigon 1
and,
a2b = a22 + b2 – c2 . . . . . . . . . eutrigon 2
Now, since the encompassing triangle is equilateral, a1 + a2 = b, and so we may substitute this expression (a1 + a2) for b in the equation for eutrigon 1 above, giving us:
a1 (a1 + a2) = a12 + (a1 + a2)2 – c2
a12 + a1 a2 = a12 + a12 + 2a1 a2 + a22 – c2
a1 a2 = c2 – a12 – a22
But this is simply our Co-eutrigon theorem in disguise, namely:
ab = c2 – a2 – b2
...We can combine these new component [integral] parts (like the intervals of the diatonic scale in music) to form a larger ‘scale structure’ which illustrates just some of the relationships and resonances between and among the component complementary eutrigons, co-eutrigons, and internal equilateral triangles [see scale structure figured below].
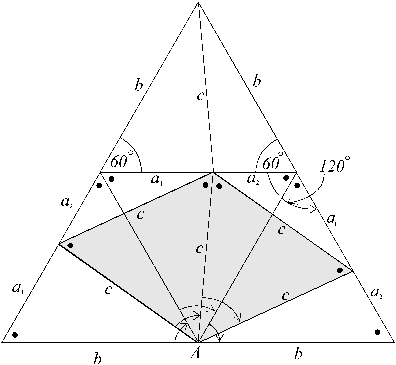
Figure ECS1
As in the earlier examples of symmetric (scale-like) constructions joined together without gaps like pieces of a jig-saw puzzle, we may expect there exist connections and resonances (hidden within the construction) not only in relation to geometry, but in relation to numbers as well. Let us remember that we are also especially considering the construction such that all lengths are in whole numbers . This imbues the figure with a ‘quantum flavour’, and may also allow for a deeper understanding of the interrelation between number and geometry, and that of the unit itself .
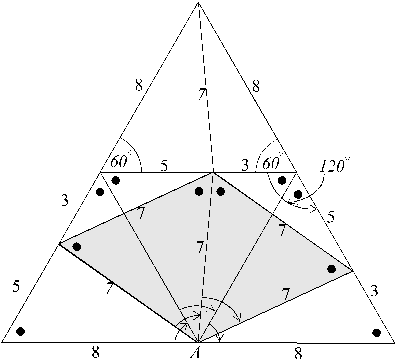
In figure ECS1 above, each of the arrowed arcs marked about point A in the centre of the base is 60°.
Also note that the central tilted-diamond (shaded in the figure) is a symmetrical rhombus (whose diameter is the same as its side lengths, and thus consists of two equilateral triangles)†. This is a resonance within this particular scale structure that persists under variations in a1 and a2 (and such that a1 + a2 = b as in Figure EP1 above).
Connections to number
We may now apply our earlier findings concerning the areas of equilateral triangles, eutrigons and co-eutrigons in etu.
Summing the component areas (in etu)
To assist in the visualisation and summing of the component isometric shapes and areas of the scale structure, I have colour-coded the congruent shapes within Figure ECS1 below (which is otherwise unchanged).
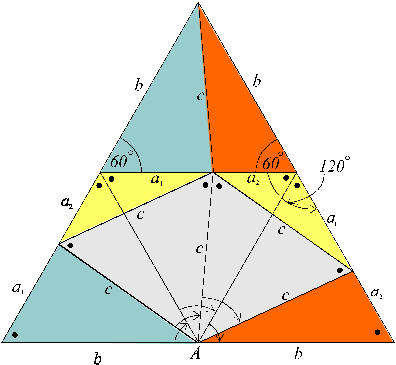
Figure ECS1-colour
It can be seen that figure ECS1-colour consists of the following congruent geometric pairs of triangles:
- two congruent aqua-coloured eutrigons plus
- two congruent orange eutrigons plus
- two congruent yellow co-eutrigons plus
- two light-grey congruent equilateral triangles.
By our reformulations for the areas of these new triangle classes in terms of relative units of area (etu), we may express this 'descriptive' summation of geometric component triangles in algebraic terms as follows:
The area of the entire figure of ECS1-colour equals,
2 a1b + 2 a2b + 2a1a2 + 2c2
That accounts for all the component areas. Noting that the overall shape is an equilateral triangle, its area can be alternatively stated (in terms of etu) as its side-length ‘squared’. Observe that the overall equilateral triangle has a side-length of 2b . Its area in etu is therefore simply (2b)2 or 4b2. So the grand tally of component areas must equal this, thus,
2a1b + 2a2b + 2a1a2 + 2c2 = 4b2
Dividing throughout by 2 we get,
a1b + a2b + a1a2 + c2 = 2b2
Since we earlier defined that a1 + a2 = b, we can substitute for b to give,
a1(a1 + a2) + a2(a1 + a2) + a1a2 + c2 = 2b2
a12 + 3a1a2 + a22 + c2 = 2b2
(a12 + 2 a1a2 + a22) + a1a2 + c2 = 2b2
(a1 + a2)2 + a1a2 + c2 = 2b2
and again, since a1 + a2 = b,
b2 + a1a2 + c2 = 2b2
thus,
a1a2 = b2 – c2
This is an interesting result arising from the figure since it directly relates to the well-known ‘difference of squares ’, b2 – c2 , and this difference may always be expressed as the product, ( b + c )( b - c ).
But the equality, a1a2 = b2 – c2, is conditional upon another relation obtained from [the figure atop this page], namely that, b = a1 + a2.
Seen from the perspective of the etu (the resonant unit of area matched to the geometry of the figure), the product a1a2 and as represented in figure ETS1, is the product of a co-eutrigon’s leg-lengths. And the product of a co-eutrigon’s leg-lengths is simply the co-eutrigon’s area in etu.
A table of new 'trigonometric identities'
—deriving from Figures ECS1, ES1, and
the Eutrigon and Co-eutrigon theorems
Given that b is a member of the eutrigon paired-triad of four integers, { (a1, a2), b , c}, and such that, a1 + a2 = b (as per the geometric construction of fig. EP1), then it follows that,
| a1b = a12 + b2 – c2 | |
| a2b = c2 – a22 – b2 | |
| a1a2 = c2 – a12 – a22 | |
| a1a2 = b2 – c2 | from Figure ECS1 |
| δ2 = 3a1b + c2 | from Figure ES1 and Eutrigon theorem |
| γ2 = 3a2b + c2 | from Figure ES1 and Eutrigon theorem |
where δ= a1 + b, and γ= a2 + b.
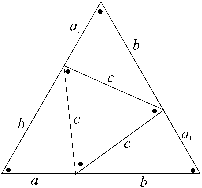
Figure ES1
The integer c is common to all the identities listed in the table, and its lowest possible value‡ is, 7. The corresponding values for this value of c are therefore:
a1 = 3
a2 = 5
b = 8
c = 7
δ = 11
γ = 13
(refer following three diagrams)
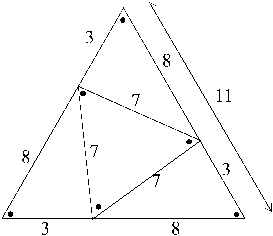
Because of our modern acceptance of rational and irrational numbers (all values in between the whole numbers), many readers may be wondering about the consequence of these whole–number solutions to the equations and geometric figures. While it is true that the equations we have been considering hold true for all other non-integral values of a1, a2, b, c, etc, this book’s perspective is to look at natural orders and relationships from the concept and premise of ‘the whole’ and as reflected in the notion of the unit . The integers, whole numbers of equal spacing or ‘equal-temperament’§, are in tune with these principles (and as covered earlier in this book). This book is directed towards the discovery of music-like resonant scale-structures, and the idea is indebted to the age-old idea of the Pythagoreans and many others ever since, that the whole Universe is like a musical scale—its overt forms unfolding like the chameleon form and flow of music itself—forever old and forever new.
The concept of the triads
It is from this perspective that we glimpse the potential importance of the Pythagorean triads, and moreover, the fact that every integer (except 1 and 2) is a member of at least one Pythagorean Triple.
So far, we have looked [above] at a specific example of a paired eutrigon–co-eutrigon triple: {(3, 5), 8, 7}, and considered some interesting connections that exist between the members of such paired-triples. But a quick test of other integral values for a1 and a2 shows that they cannot be any integer—many integral values will generate non-integral values for the hypotenuse c. There must exist some underlying pattern that we still need to elucidate in order to generate other paired-triples in which the same relations (as given by the tabulated equations above) hold true—in other words, we need to find parametric equations (similar to those the Pythagoreans found) that will output integer sets (i.e. paired triples) for our eutrigons.
Parametric Equations** to generate Eutrigon–Co-eutrigon paired triples
First, we redraw our figure (EP1) of the paired eutrigons which may be joined along their common hypotenuse to form an equilateral triangle.
Figure EP1 (repeated)
Paired Eutrigon-triples** of integers for a1, a2, b , and c, of figure EP1 are given by:
|
where p is an integ  er 3 and q is another integer such that q < p/2 |
a2 = 2pq – q2 |
|
b = p2 – q2 |
|
c = p2 + q2 – pq |
Testing these for (say): p = 3 and q = 1,
we get values for a1 , a2 , b, and c as follows,
a1 = p2 – 2pq gives a1 = 9 – 6 = 3
a2 = 2pq – q2 gives a2 = 6 – 1 = 5
b = p2– q2 gives b = 9 –1 = 8
c =p2 + q2 – pq gives c = 10 – 3 = 7
These values for a1, a2, b, and c, all agree with our first pair of eutrigons in integral sides (and of lowest possible integral values).
Let’s try some other random higher inputs for p and q:
Let p = 8, then q < 4 (as q must be < p/4), so let’s make q = 3.
Therefore by our parametric equations give:
a1 = p2 – 2pq = 64 – 48 = 16
a2 = 2pq – q2 = 48 – 9 = 39
b = p2– q2 = 64 –9 = 55
c =p2 + q2 – pq = 64 + 9 – 24 = 49
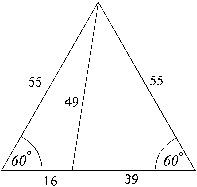
The above figure shows the second example of paired eutrigon triads in geometric formation.
| back to top |
next > |