Escher - underrecognised genius of twentieth century art
Maurits Escher (1898-1970) was one of those rare artists in the tradition of Leonardo da Vinci— each approached their art as if it were also a science. And each studied the sciences from an artistic perspective.
Escher was an amateur mathematician, although you would not think so from a survey of the methodical diagrams he set out in his notebooks on the regular division of the plane. This, in my own estimation, is his single most important contribution to the future of art. Almost single-handedly he united geometry, number and art so logically that he fitted them together literally as pieces of a jig-saw puzzle. He visually explored the concepts of infinity and of impossible yet mathematically-conceivable geometric figures.
In light of the present discussion and terminology used in this document and theory, his study of the geometric divisions of the plane stands as one of the seminal contributions to art history in that it elucidates and explores one of the first and most fundamental of 'scale structures' directly applicable to the visual arts — that of the regular division of the plane, and whose power I believe we will see implemented within artistic practice in the very near future, brought to life in a new dynamic and interactive visual art form founded on interconnecting scale structures and the syntaxes which unite them, thus paralleling, in principle, the composition of music.
Escher showed that, ‘Every interlocking jigsaw-puzzle pattern of congruent pieces and which repeats in such a way that every piece is surrounded in the same way, can be associated with one of the six geometric regular divisions shown in his illustrations: of parallelograms, of rectangles, of squares, of triangles, of 60o rhombuses, or of regular hexagons…’ (D. Schattschneider, 1990, p.31) These six can be further simplified into two types: quadrilateral systems and, triangle systems . |
|
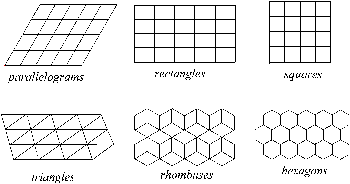
The six fundamental regular divisions of the plane
| back to top |
next > |