Relative units: the 'standing waves' of space-time, and 'natural resonances' within Nature's scale structures
The time is ripe for complete relativity
| ...the dimensionless constants such as pi, e and the new Feigenbaum constant, should reflect this ultimate 'metric' of the Universe, and should be keys to an understanding of Universal form and scale (just as the time it takes for an echo to return tells you the distance to the reflecting wall). These dimensionless constants (such as pi ) reflect the whole; they 'divide' the whole, in extremely beautiful and resonant ways. This scale structure, this division, reflects the undivided, the great Unity of all and everything. It seems likely that ultimately the new theories of physics and cosmology, in short the New Science, will be expressed in terms of dimensionless numbers, 'ideas' and 'pictures'. The units-of-measure which currently litter our scientific equations is indication of their failure as adequate expressions of the Universal connection of the whole. Many create false or artificial reference frames which distort the underlying dynamic interrelationships. They also often create the need for 'constants' within the equations of physics: a signal of mismatched units and remainders. For instance, the speed-of-light to be expressed as so-many-kilometres per second is ludicrous. 'Seconds' , 'minutes' and 'hours' confuse and cloud the 'cosmic connecting principles' by introducing a completely arbitrary non-resonant division or metric into the equations of physics. We must and will find other ways of expressing light and time perhaps within a new language of connected and interdependent principles and forms. Einstein’s relativity is like new wine in old wineskins. When we further explore the profound relativity of all and everything, then we will find ways of expressing something in terms of something else, without the need to resort to arbitrary 'units of measure'. |
|
Relative units
We have traditionally expressed areas in terms of square units. It is now apparent that areas can be expressed in triangular units, in hexagonal units, or in any units which can tile the plane without gaps (e.g. any triangle can tile the plane). The units we choose depend on the situation and context. Thus is introduced the notion of relative units .
Why all the fuss when square units have done such a fine job for so long? The answer will become apparent as we consider the nature of numbers and geometries. The application of appropriate units to a problem simplifies the mathematics and reveals a more beautiful connectedness. The answer has to do with wholeness, simplicity, and connection; the connection of numbers to the shape of space; of quantity to quality. In a fundamental way it has to do with universal organisation.
Let's summarise some important points we need to grasp here:
- Areas can be expressed in different ways depending on the units we choose (square, triangular, hexagonal, etc). An area of nine square-units is not the same absolute area as nine triangular-units (i.e. equilateral triangles) even though the numbers are the same. In other words, we note that a 3 x 3 square has a greater absolute area than a 3 x 3 equilateral triangle. The traditional perspective has been to emphasise the differences between them (in terms of absolute areas).
- But this difference is balanced by its very opposite: an equivalence principle of great beauty. The equivalence becomes clear when you ignore the artifice of arbitrary units (inches, ...centimetres, etc) and focus instead on the pure numbers and on the relative units of shape enclosed by each (Fig. 51). For a given side length p (expressed in pure numbers) the area in each of these systems (expressed in terms of the number of enclosed self-similar shape-units) is the same in each, p2. This relation we have shortsightedly described as ‘the square of the side’ . Stop for a minute and let this point sink in. The number ‘4’, for example, can just as comfortably represent any of several different shapes (a square in a square system; a triangle in a triangle system, etc). And these shapes occupy different amounts of space (area) on the plane. But in each, the number ‘4’ has the same relative meaning: a regular polygon of side-length 2 (square, equilateral triangle or hexagon), with an area of 2 x 2 (or 22) relative units [see scale structure of the plane & fig. 51, below].
- So, these 'square numbers' (1, 4, 9, 16...) need not necessarily be associated with squares, and only squares. The same numbers are equally at home in the shape of equilateral triangles or hexagons, and in fact can be associated with other less regular shapes which can tile the plane, as we shall see.
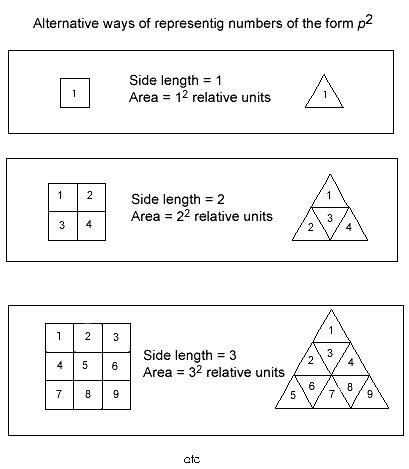
Figure 51
A new name needed for the ‘square numbers’?
A new word is clearly needed for these special numbers of the form p2 and hitherto known simply as ‘the squares’. Perhaps we might call them ‘syms’ (pronounced, sims).
Sym is a root which, in relation to these numbers, might have the following meanings:
Symmetry ~e.g. of polygons, algebraically, p x p
Symphysial ~lines of gapless articulation can be formed between adjacent self-similar shapes, rather than being restricted to mere points of contact which may be the only possible form of connection between ' non-resonant' shapes
Symbolic ~can be variously represented
Symphonic ~harmonious combination of elements or parts; having a 'musical' scale structure
Symbiotic ~mathematics synergized by appropriate use of the full complement of their forms
Sympathetic ~have 'fluid' characteristics allowing them to adapt and change their shape according to different situations.
It is to be anticipated that the full adoption of the principle of relativity (even at the conceptual level of the unit) will profoundly alter our understanding of the Universe in an expansive way.
| back to top |
next > |